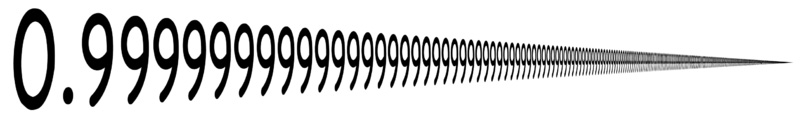Q: Is 0.9999… repeating really equal to 1?
Mathematician: Usually, in math, there are lots of ways of writing the same thing. For instance:
= 
= 
= 
= 
As it so happens, 0.9999… repeating is just another way of writing one. A slick way to see this is to use:
One.
Another approach, that makes it a bit clearer what is going on, is to consider limits. Let’s define:
…
and so on.
Now, our number 
is bigger than 
for every n, since our number has an infinite number of 9′s, whereas always has a finite number, so we can write:
is bigger than for every n, since our number has an infinite number of 9′s, whereas always has a finite number, so we can write:
for all n.
Taking 1 and subtracting all parts of the equation from it gives:
Then, we observe that:
and hence
.
But we can make the left hand side into as small a positive number as we like by making n sufficiently large. That implies that 1-0.9999… must be smaller than every positive number. At the same time though, it must also be at least as big as zero, since 0.9999… is clearly not bigger than 1. Hence, the only possibility is that
and therefore that
.
What we see here is that 0.9999… is closer to 1 than any real number (since we showed that 1-0.9999… must be smaller than every positive number). This is intuitive given the infinitely repeating 9′s. But since there aren’t any numbers “between” 1 and all the real numbers less than 1, that means that 0.9999… can’t help but being exactly 1.
Update: As one commenter pointed out, I am assuming in this article certain things about 0.9999…. In particular, I am assuming that you already believe that it is a real number (or, if you like, that it has a few properties that we generally assume that numbers have). If you don’t believe this about 0.9999… or would like to see a discussion of these issues, you can check this out.
